파이썬 통계분석_Chpater08. 대표적인 연속형 확률분포

이 장에서는 정규분포를 비롯하여 추정이나 검정을 수행할 때 사용하는 분포를 다양하게 살펴볼 것이다.

** 분포의 형태나 성질을 확실히 파악해두자.

 

- 라이브러리 임포트

 

- 연속형 확률분포의 성질을 확인하기 쉽도록 몇 가지 함수를 미리 준비

- check_prob는 확률변수를 인수로 취하여 그 확률변수가 확률의 성질을 만족하는지 확인하고, 기댓값과 분산을 계산하여 반환하는 함수

- plot_prob는 확률변수와 구간을 인수로 취하고, 그 확률 변수의 밀도함수와 분포함수를 그리는 함수

 

정규분포(normal distribution)는 통계분석에서 매우 자주 사용되는 중요한 확률분포로, 자연계에서 일어나는 수많은 현상을 표현할 수 있다.

가우스 분포(Gaussian distribution)라고도 부른다.

정규분포가 취할 수 있는 값은 실수 전체이다.

* 표준편차의 제곱이 분산

정규분포에는 다른 확률분포에는 없는 매우 중요한 성질이 있다.

정규분포를 따르는 확률변수 X를 aX+b와 같이 변환한 경우, 변환한 확률분포도 정규분포를 따른다는 것이다.

표준화한 정규분포 N(0,1)을 표준정규분포(standard normal distribution)라 부른다.

 

- Numpy를 사용해 정규분포 변환 함수 구현

 

- N(2, 0.5^2)을 따르는 확률 변수 X 작성, 기댓값과 분산 계산

 

- 밀도 함수와 분포함수를 0과 4 사이의 구간에서 그림, 정규 분포의 밀도함수는 좌우 대칭인 종 모양이 되는 것이 특징

 

- 정규 분포를 따르는 함수는 norm함수로 생성, 첫 번째 인수에 기댓값, 두 번째 인수에 표준편차를 각각 지정

- 각각 기본 설정값이 0, 1이므로, 아무것도 지정하지 않으면 표준 정규 분포를 따르는 확률 변수가 생성

- 기댓값이 2이고 표준편차가 0.5인 정규 분포를 따를 확률 변수를 생성

- 기댓값과 분산은 각각 mean과 var 메서드로 구할 수 있다

 

- 밀도 함수는 pdf메서드로 계산

- P(X = 2)라는 확률을 구하는 것이 아님

 

분포 함수는 cdf 메서드로 계산할 수 있다.

분포 함수는 P(X <= x)를 계산하는 함수이다.

- cdf 메서드를 사용하여, X가 1.7보다 작은 값이 되는 확률 P(X <= 1.7)

 

isf 메서드를 사용하면 상위 100α%점(upper 100α% point)을 구할 수 있다.

상위 100α%점이란 P(X>= x) = α를 만족하는 x로, 왼쪽 끝의 x좌표에 해당한다.

- isf 메서드를 사용하여 상위 30%점을 구함

 

interval 메서드로 확률이 α가 되는 가운데 부분의 구간을 구할 수 있다.

이 때 오른쪽과 왼쪽에서 남은 부분의 면적은 동일하다.

즉 a와 b는 P(a<= X <= b) =α를 만족하고, P(X <= a) = P(X>=b) = (1- α)/2를 만족한다.

- interval 메서드를 사용하여 90% 구간을 구함

 

- 오른쪽과 왼쪽에 5%씩 남아 있기에, a와 b를 다음과 같이 구할 수 있다

- stats.norm을 사용, 파라미터에 따라 정규분포의 형태가 변화

- N(0,1), N(0,4), N(1,1)의 세가지 정규분포

 

분산이 커짐에 따라 분포가 넓어지고, 기댓값이 변화하면 분포 전체가 평행이동한다.

 

지수분포(exponential distribution)는 어떤 사건이 발생하는 간격이 따르는 분포이다.

간격이라는 시간이 따르는 분포이므로, 확률변수가 취할 수 있는 값은 0 이상의 실수이다.

지수분포는 단위시간당 평균 발생하는 사건의 발생 간격을 따르는 확률분포이다.

ex) 하루당 평균 2건의 교통사고가 발생하는 지역에서 하루 교통사건 발생 간격, 1시간당 평균 10번 액세스하는 사이트에 대한 액세스 간격

 

- Numpy로 지수 분포의 밀도함수 구현

- Ex(3)을 따르는 확률 변수 X 작성

- 기댓값은 1/3, 분산은 1/9이 된다

 

- 0부터 2사이의 구간에서 밀도함수와 분포함수를 그림, 지수분포의 밀도함수는 값이 커질수록 지수적으로 감소

- scipt.stats에서는 지수분포를 따르는 확률변수를 expon함수로 작성할 수 있다

 

파라미터 값이 커짐에 따라 확률분포는 점점 감소하는 것을 알 수 있다.

 

카이제곱분포(chi-square distribution)는 분산의 구간 추정이나 독립성 검정에서 사용되는 확률분포이다.

카이제곱분포가 취할 수 있는 값은 정의에서 알 수 있듯이 0이상인 실수이다.

- 표준정규분포에서 표본 크기 10으로 무작위추출을 하여 그 제곱합을 취하는 작업을 100만 번 수행한다

- 무작위추출한 표본 크기 100만의 표본 데이터를 얻을 수 있다

 

10개의 표준정규분포 제곱합이므로 자유도가 10인 카이제곱분포가 된다.

scipy.stats에서는 카이제곱분포를 따르는 확률변수를 chi2함수로 생성할 수 있다.

첫 번째 인수에 자유도를 지정하고, 이것을 이용하여 무작위추출한 표본 데이터의 히스토그램과 밀도 함수를 함께 그려보자.

 

- 히스토그램과 밀도함수가 정확하게 일치한다는 것을 확인할 수 있다

 

카이제곱분포가 자유도 n에 따라 어떠한 분포 형태가 되는 지 살펴보자.

- 자유도 n을 3, 5, 10으로 변화

 

카이제곱분포의 특징 세가지

01. 좌우 비대칭으로, 왼쪽으로 치우치고 오른쪽으로 넓어진다.

02. 자유도가 커지면 좌우대칭에 가까워진다.

03. 자유도의 값 가까이에 분포의 정점이 있다.

 

isf메서드를 사용하면 카이제곱분포의 상위 100α%점은 다음과 같이 구할 수 있다.

- 자유도가 5인 카이제곱분포의 상위 5%

 

t분포(t distribution)는 정규분포에서 모평균의 구간추정 등에 사용되는 확률분포이다.

t분포가 취할 수 있는 값은 실수 전체이다.

- 자유도가 10인 카이제곱분포를 사용했으므로, 자유도가 10인 t분포가 생성

- scipy.stats에서는 t분포를 따르는 확률변수를 t함수로 생성할 수 잇고, 인수에 자유도를 지정한다.

 

- 무작위추출한 표본 데이터의 히스토그램과 t(10)의 밀도함수

 

t분포가 자유도 n에 따라 어떤 분포 형태가 되는 지 살펴보자.

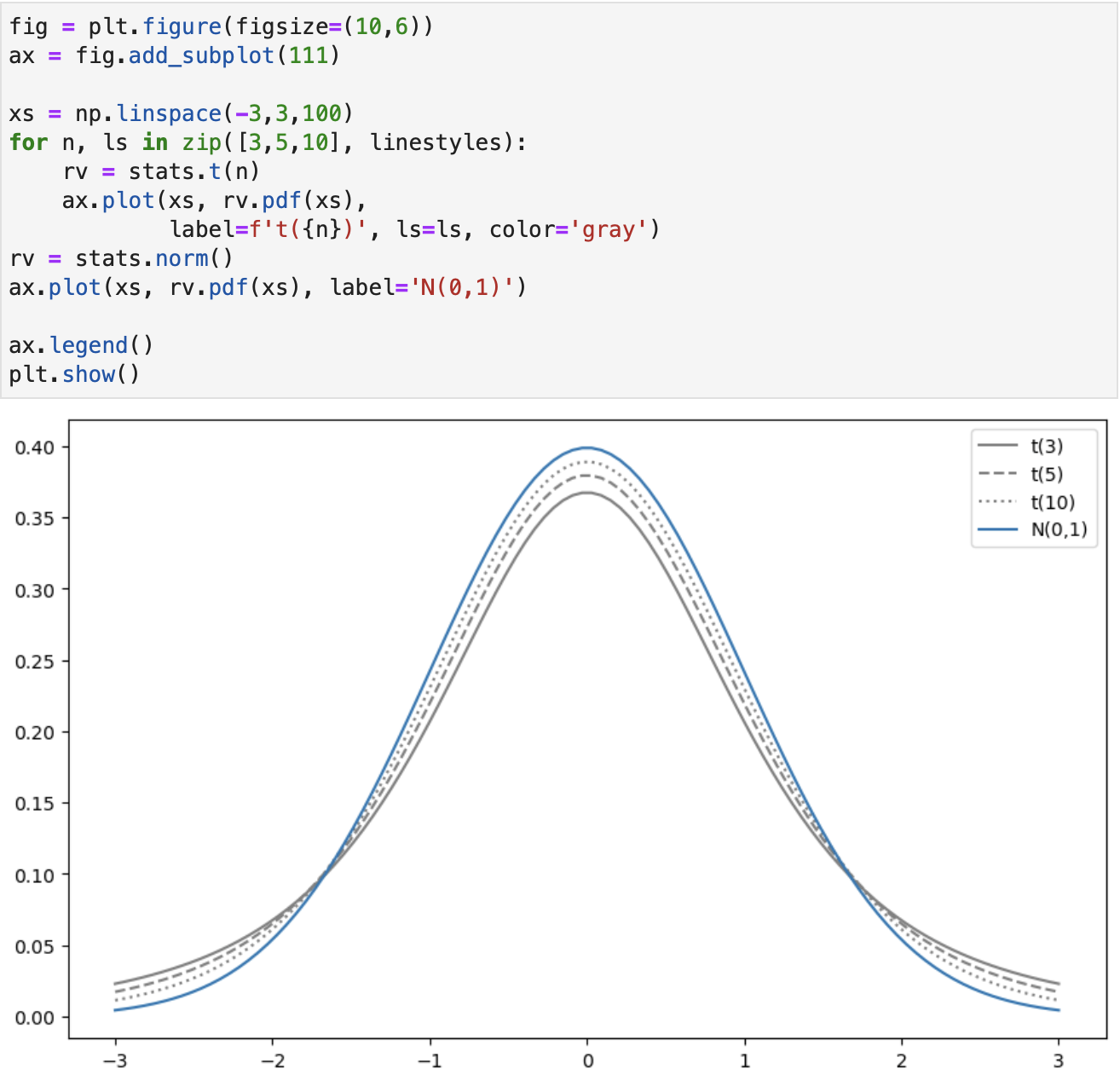
- 자유도 n을 3, 5, 10으로 변화, 비교를 표준정규분포도 함께 그림

 

t분포의 특징 세가지

01. 좌우대칭인 분포이다.

02. 표준정규분포보다 양쪽 끝이 두껍다.

03. 자유도가 꺼지면 표준정규분포에 가까워진다.

 

- 자유도가 5인 t분포의 상위 5%

 

F 분포(F distribution)는 분산분석 등에서 사용되는 확률분포이다.

F 분포가 취할 수 있는 값은 0 이상인 실수이다.

- 자유도가 5, 10인 F 분포

- 무작위추출한 표본 데이터의 히스토그램과 함께 F(5,10)의 밀도함수

 

다음으로 F 분포가 자유도의 변화에 따라 어떤 형태의 분포가 되는 지 살펴보자.

- 자유도 n2는 10으로 고정하고, n1을 3, 5, 10으로 변화

 

F 분포의 특징 두가지

01. 좌우 비대칭으로, 왼쪽으로 치우치고 오른쪽으로 넓어지는 분포이다.

02. 분포의 정점은 1에 가깝다.

 

 

누구나 파이썬 통계분석[타니아이 히로키] 참조